The Vehicle Routing Problem Explained
Posted by Nathalie Göbel on 11/07/2022

Every day, managers of last mile delivery are responsible for getting goods from place A to B, effectively and efficiently. Quite simple right? Actually, there is more to it than meets the eye. Imagine having hundreds or even thousands of orders a day, with one hundred trucks at your disposal. How are you going to place each order on a route, taking into account all restrictions and time windows, while minimizing the total cost? This is exactly the question of a Vehicle Routing Problem.
What is the Vehicle Routing Problem (VRP)?
Most people have a basic understanding of what the Vehicle Routing Problem is. In essence, it is the challenge of determining optimal routes from a depot to a set of geographically dispersed customers in order to fulfil known customer requirements. The main objective of the VRP is to minimize distribution costs, however the amount of complexity involved when solving this problem is often underestimated.
VRP is not a new phenomenon as it goes all the way back to the mid-20th century. It first appeared in a paper written by George Dantzig and John Ramser in 1959, in which this algorithmic problem was first applied in the context of petrol delivery. Back then, mathematicians applied manually calculated route optimization algorithms to find the most optimal routes for a set of vehicles. Nowadays, technology provides tremendous support in this field in the form of route optimization software. Thanks to high speed algorithms, logistics providers are able to optimize their VRP in minutes.
Traveling Salesman Problem (TSP)
A classic, well-known example of a VRP is the Traveling Salesman Problem (TSP). TSP concerns finding the shortest route a salesperson or vehicle can take, given a list of specific destinations which can only be visited once. Notice that when talking about TSP, there is only one vehicle in the equation. As soon as multiple vehicles come into play, it becomes a VRP. This is illustrated below.
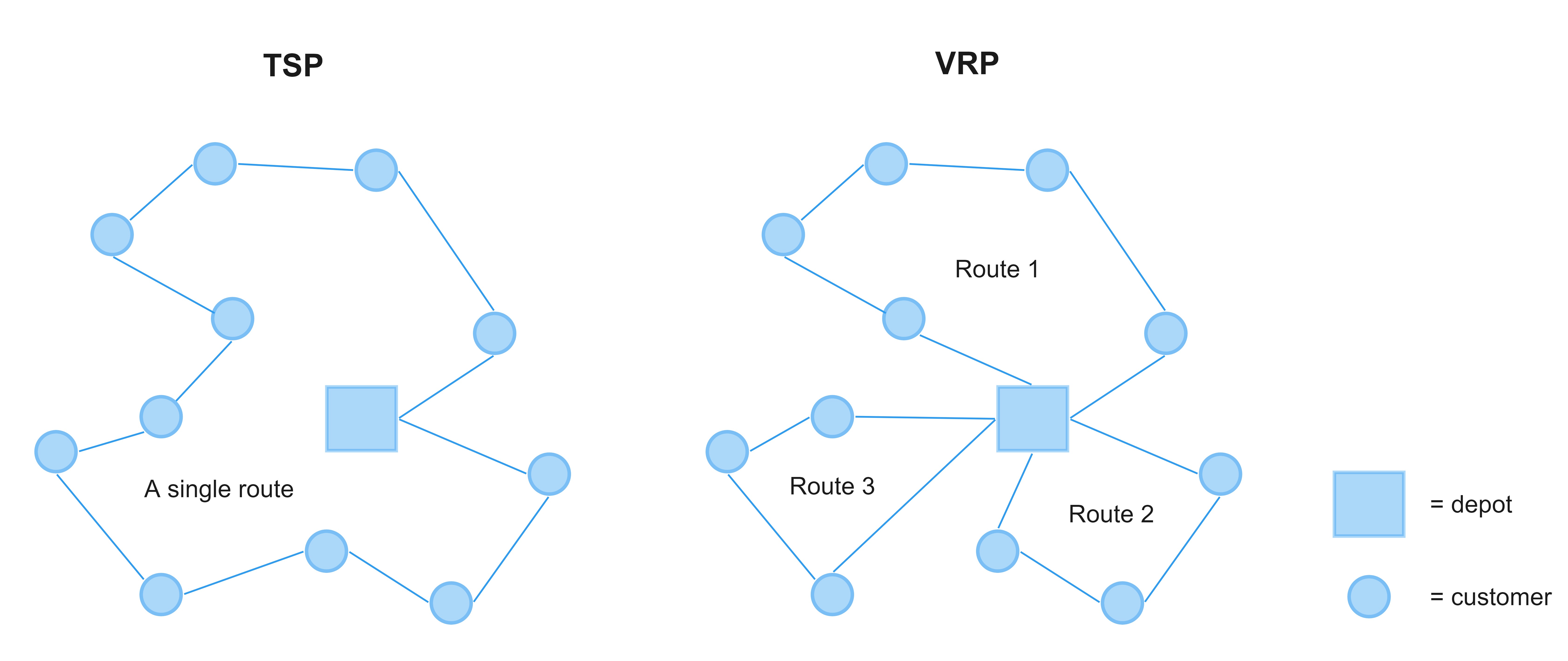
Why is it such a challenge to solve VRP?
In real-life scenarios, it is not only about finding the shortest route possible. There are numerous other components that contribute to planning optimal routes. The complexity of VRP emerges when multiple constraints need to be taken into account. The most common ones are explained below:
Capacity
Every vehicle has a carrying capacity, meaning that it can only carry a certain number of items at once, without exceeding the threshold volume and weight. The objective is to create a route that allows a vehicle to pick up/deliver the maximum quantity at the lowest costs within the available capacity. The level of complexity can vary greatly between businesses. Whereas a general logistics provider could transport cargo ranging from food, to electronics and furniture, a fashion retailer usually only transports garments. For the logistics provider, the same truck may have different capacity specifications depending on the type of good being carried. The fashion retailer on the other hand, may only have one category, making the capacity specifications a lot more simplified.
Time windows
Time windows indicate when each visit can be performed and therefore add another layer of complexity to the puzzle. Each customer and depot often have their own specific opening hours that vary throughout the week, which all need to be taken into account when solving a real-life VRP.
Pickup and Delivery
A pickup and delivery VRP arises when a vehicle has to collect goods or people from various locations and drop them off at several destinations points. The principal challenge is to optimally combine the transportation of all goods (or people) while minimizing the total length of the route. In most cases, the pick-ups and deliveries occur sequentially, meaning there is no depot involved.
Resource constraints
Resources are limited, but highly necessary for the delivery of goods. Your vehicle routing problem will therefore always have to take into account the available number of drivers/ vehicles and working hours, in order to achieve a realistic solution.
Benefits of solving VRP
However complex VRP may be, effectively solving it is extremely beneficial for any road transport operation, since it improves vehicle’s utilization. This means it enables companies to transport more in one go. Consequently, the total fleet travel time will be reduced resulting in substantial cost savings and less CO2-emissions, which is now more important than ever.
How to solve VRP
Today we still see many companies trying to tackle VRP manually or with the aid of some basic tools. However, we must be realistic. As the number of possible combinations in a vehicle routing problem quickly runs up into the billions, you can imagine that solving it manually is the least effective option. The number of calculations that are necessary to solve VRP make a planner’s job nerve-wracking and time-consuming, and we must not forget there’s a high chance of mistaking data during this manual process. In addition, real-world planning involves a large variety of constraints that make it nearly impossible for the human brain to figure out a close to optimal solution, let alone find a solution.
Using advanced computing power in the form of route optimization software, is by far the best way to go. This eliminates all manual calculations and automatically generates an optimal route in seconds. In addition, it elevates the role of the planner to a more analytical one, where adjustments can be made based on expertise and experience.
Conclusion
In conclusion, VRP is an extremely complex algorithmic problem that has been studied extensively for more than 60 years. Although it is not a new phenomenon, finding an optimal solution remains a challenge. Today’s distribution networks have a high level of complexity and fuel prices are soaring, making it critical for companies to search for more efficient ways to solve VRP. Route optimization software provides today’s logistics providers with the opportunity to utilize their resources to the maximum, saving them time, money and unnecessary emissions.

